36 PAA - Problémy a algoritmy

Úloha 1: Řešení problému batohu

Zadání

Naprogramujte řešení 0/1 problému batohu hrubou silou. Na zkušebních datech pozorujte závislost výpočetního času na n.
Naprogramujte řešení 0/1 problému batohu heuristikou podle poměru cena/váha. Pozorujte
- závislost výpočetního času na n
- průměrné zhoršení proti exaktní metodě
- maximální chybu.

Specifikace problému

Problém batohu by se dal popsat následujícími matematickými formulacemi.

Je dáno

celé číslo n (počet věcí)
celé číslo M (kapacita batohu)
konečná množina V={v₁, v₂, ... ,v_n } (hmotnosti věcí)
konečná množina C={c₁, c₂, ... ,c_n } (ceny věcí)

Zkonstruujte množinu X={x₁, x₂, ... ,x_n }, kde každé x_i je 0 nebo 1, tak, aby

platilo
v₁x₁+v₂x₂ + ... + v_nx_n <= M

(batoh nebyl přetížen).
výraz
c₁x₁+c₂x₂ + ... + c_nx_n

nabýval maximální hodnoty pro všechny takové množiny (cena věcí v batohu byla maximální).

Řešení problému

Jelikož se jedná o NP těžkou úlohu, jejíž složitost roste exponenciální řadou, je pro řešení problému možno využít několik způsobů. V této úloze bude využita metoda hrubé síly a jednoduchá heuristika.

Hrubou silou

Tento způsob je nejjednodušší na implementaci, avšak jeho výpočetní složitost roste řádově exponenciálně, jelikož se uvažují všechny kombinace věcí dané instance. Pro ořezání stavového prostoru se využívá maximální nosnost batohu, kdy se již do batohu nepřidávají další věci v příslušné kombinaci. Zároveň se testuje, zda nově získaná hodnota ceny věcí v batohu nepřesahuje dosavadní maximum, v tom případě se provede aktualizace maxima.

Heuristika s využitím poměru cena/váha

Druhý způsob řešení je postaven na jednoduché heuristice, kdy se využívá poměr cena/váha. Vychází se z logického Úsudku, že nejdříve je nutné postupně vkládat do batohu ty nejdražší věci s co nejmenší hmotností až do zaplnění batohu. Nejdříve je nutné danou instanci setřídit podle poměru cena/váha a pak postupně přidávat věci až do nosnosti batohu. Toto řešení nabízí, jak se ukáže v naměřených hodnotách, velmi dobrou časovou složitost. Otázkou však zůstává, zda se podaří najít vždy to nejlepší řešení.

Naměřené hodnoty

Pro výpočet řešení a měření byla využita následující konfigurace:

Intel Pentium IV Dual Core 2Ghz, 1.5GB RAM, operační systém Mac OS X Tiger 10.4.10

Po průchodu algoritmu instancemi o různých dimenzích jsem získal následující naměřené hodnoty, ze kterých jsem určil i průměrné zhoršení heuristiky oproti exaktní metodě a maximální chybu.

N	Hrubá síla [s]	Heuristika [s]	Prům. zhoršení [%]	Max. chyba
4	<0.01	<0.01	2.5	84
10	<0.01	<0.01	1.9	121
15	0.01	<0.01	1.1	52
20	0.25	<0.01	0.5	107
22	1.09	<0.01	0.32	80
25	9.96	<0.01	0.71	76
27	43.51	<0.01	0.54	61
30	390.72	<0.01	0.61	64
32	1677.3	<0.01	0.23	60
35	1862.8	<0.01	0.19	59
37	1974.5	<0.01	0.82	73
40	2200.2	<0.01	0.42	68

Tabulka 1: Naměřené hodnoty

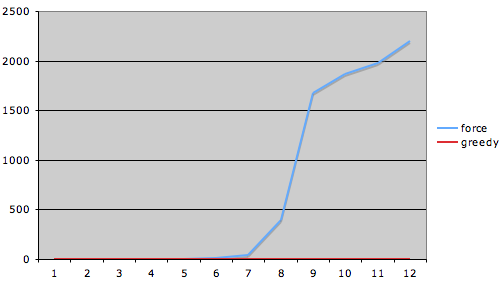
Naměřené hodnoty jsem pro větší názornost vynesl do grafu.

Závěr

Řešení hrubou silou rostlo dle očekávání exponenciální řadou, tedy se složitostí O(n . 2ⁿ) a je velmi závislé na velikosti instance, což se pro větší dimenze stává problematické.

Na druhou stranu, řešení pomocí heuristiky dávalo výborné časové výsledky, v této Úloze prakticky neměřitelné, pro různě velké instance, u kterých je algoritmus hrubé síly prakticky nepoužitelný. Nevýhodou je fakt, že ne vždy je možné najít to nejlepší řešení. Dává však vcelku uspokojivé výsledky, jak je patrné z průměrného zhoršení.

Příloha

Ke stažení je k dispozici zabalená celá úloha, nebo jen zdrojový kód vytvořený v programovacím jazyku C: