36 PAA - Problémy a algoritmy

Úloha 6: Řešení problému vážené splnitelnosti booleovské formule simulovaným ochlazováním

Jan Dohnal (dohnaj1@fel.cvut.cz)

Zadání

Řešte problém vážené splnitelnosti booleovské formule některou z následujících metod: lokální metoda pomocí záměn, simulované ochlazování, genetický algoritmus, tabu prohledávání. Je dána booleovská formule F proměnnných X=(x 1, x2, ... , xn) v konjunktivní normální formě (tj. součin součtů). Dále jsou dány celočíselné kladné váhy W=(w 1, w2, ... , wn). Najděte ohodnocení Y=(y 1, y2, ... , yn) proměnných x1, x2, ... , xn tak, aby F(Y)=1 a součet vah proměnných, které jsou ohodnoceny jedničkou, byl maximální. Je přípustné se omezit na formule, v nichž má každá formule právě 3 literály (problém 3 SAT). Takto omezený problém je stejně těžký, ale možná se lépe programuje a lépe se posuzuje obtížnost instance (viz Selmanova prezentace v odkazech).

Použitá metoda

Pro řešení této úlohy jsem zvolil metodu simulovaného ochlazování. Jedná se o jednu z pokročilých iterativních metod pro řešení NP problémů. Využívá se postupného „snižování teploty“, kdy teplota ovlivňuje pravděpodobnost přijmutí nového stavu zhoršujícího optimalizační kritérium současného řešení. Pokud je teplota vysoká, pravděpodobnost přijmutí stavu, který má horší optimalizační kritérium než současný stav, je vyšší, než v případě nízké teploty. Tedy pokud je teplota vysoká, pravděpodobnost akceptace stavu, který má horší optimalizační kritérium než současný stav je vyšší, než pokud je teplota nízká.

Řešení

Omezil jsem se na řešení takových formulí, v nichž má každá formule právě 3 literály (problém 3 SAT). Takto omezený problém je stejně těžký, ale možná se lépe programuje a lépe se posuzuje obtížnost instance (viz Selmanova prezentace v odkazech). Program má uloženou formuli s odpovídajícím ohodnocením jednotlivých proměnných, na které poté provádí algoritmus simulovaného ochlazování. Pro ochlazování se využívá multiplikativní koeficient alfa. Ve vnitřním cyklu se testuje podmínka na maximální počet iterací.

Generování počátečního řešení: počáteční řešení je zvoleno náhodně pomocí funkce pro náhodné vygenerování sousedního řešení. Hodnoty proměnných se na začátku nastavují na 0 a následně se hledá sousední řešení.
Generování sousedního řešení: sousední řešení je platná sousední konfigurace proměnných, tedy při změně hodnoty jedné proměnné. Inkrementálně se pak vyzkouší změna každé další proměnné.
Cena: cena je součet ohodnocení proměnných s hodnotou 1 – tedy S.

Nastavení parametrů

Parametry simulovaného ochlazování ovlivňující běh algoritmu a výsledek jsou tyto:

t0 (počáteční teplota) - má vliv na přijetí horšího stavu (nižší teplota znamená nižší pravděpodobnost přijetí horšího stavu). Nižší hodnota znamená rychlejší konvergenci.
α (koeficient ochlazování) - ovlivňuje snižování teploty. Je nutné najít optimální hodnotu pro kvalitní výsledky.
i (práh iterace) - práh iterace určuje konec algoritmu. Pokud nedojde ke změně po stanovený počet iterací, algoritmus skončí. Vyšší hodnota umožňuje dosáhnout lepších výsledků.

Ochlazování	T = T * α, kde α ə {0.80, 0.82, ... 0.98}
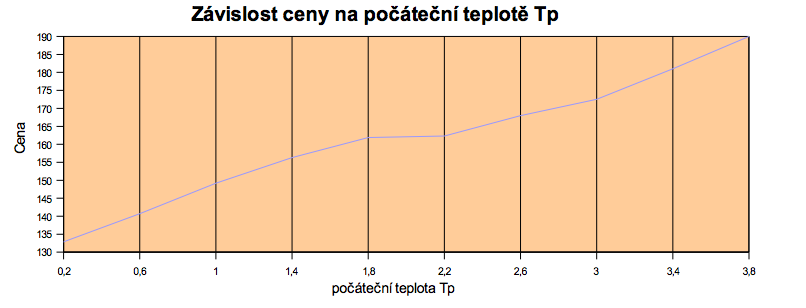
Počáteční teplota	T_p = {0.2,0.6,1,1.4,1.8,2.2,2.6,3,3.4,3.8}
Koncová teplota	T_k = 0.1
Equilibrium	Když počet iterací 1000
Práh iterace	1

Popis kostry algoritmu

ohodnoceni = new int[n]; 
nove_ohodnoceni = new int[n]; 
temp = start_temp; 
cena = gen_init(ohodnoceni); 
printf("Initial state: "); 
print_conf(ohodnoceni); 
//simulovane ochlazovani 
while ((temp > stop_temp) && (iter_nochange < prah_iter)) 
{ 
minula_cena=cena; 
for (unsigned int i=0;i<max_iter;i++) 
{ 
tmp_cena = try_state(temp,cena,ohodnoceni,nove_ohodnoceni); 
if (tmp_cena) 
{ 
tmp=ohodnoceni; 
ohodnoceni=nove_ohodnoceni; 
nove_ohodnoceni=tmp; 
cena=tmp_cena; 
} 
} 
//ochlazeni 
temp*=alfa; 
//zjstime jestli se zmenila cena 
iter_nochange = (minula_cena == cena) ? iter_nochange + 1 : 0; 
}

Algoritmus pracuje se statickým dvourozměrným polem pro uložení celé formule, kde v jedné dimenzi jsou uloženy jednotlivé literály a v druhé dimenzi pak podformule. V dalším poli jsou pak uložena ohodnocení proměnných.

Naměřené hodnoty

Měření probíhalo na počítači Intel Pentium IV Dual Core 2Ghz, 1.5GB RAM, operační systém Mac OS X Tiger 10.4.10. Program je napsán v jazyce C++ a kompiloval se v g++.

t0	α	konečná cena	navštíveno stavů	akceptováno stavů	akceptováno zhoršení	t0	α	konečná cena	navštíveno stavů	akceptováno stavů	akceptováno zhoršení
0,2	0,80	140	9195	1260	620	2,2	0,80	168	20205	8048	4014
	0,82	138	9690	1376	677		0,82	166	19395	8465	4223
	0,84	138	10365	1506	743		0,84	167	21525	9378	4679
	0,86	135	10830	1632	806		0,86	166	23700	10535	5258
	0,88	136	12240	1851	914		0,88	165	24945	11628	5805
	0,90	135	12795	2027	1002		0,90	161	28650	13905	6944
	0,92	131	13890	2352	1166		0,92	160	33570	16914	8448
	0,94	128	14970	2811	1395		0,94	159	37350	20247	10116
	0,96	127	16575	3372	1676		0,96	158	45405	25806	12896
	0,98	121	20445	4598	2289		0,98	153	59010	37731	18860
0,6	0,80	145	13020	3162	1569	2,6	0,80	172	19230	8558	4269
	0,82	144	14055	3564	1770		0,82	172	20400	9326	4653
	0,84	144	14760	3858	1919		0,84	170	23865	10613	5295
	0,86	141	16095	4343	2162		0,86	170	25215	11754	5867
	0,88	140	16590	4730	2355		0,88	171	29970	14046	7013
	0,90	141	18735	5657	2819		0,90	171	29565	15002	7491
	0,92	140	21720	6615	3297		0,92	168	32400	17298	8640
	0,94	140	24315	7961	3971		0,94	166	45870	24159	12071
	0,96	137	28755	10379	5180		0,96	161	49845	29549	14766
	0,98	135	31680	13082	6533		0,98	159	70125	45473	22730
1	0,80	155	14340	4638	2309	3	0,80	178	20115	9060	4520
	0,82	156	16110	5103	2541		0,82	174	21870	10236	5108
	0,84	151	18795	5960	2970		0,84	174	23250	11205	5592
	0,86	150	18480	6258	3119		0,86	173	27045	13073	6527
	0,88	150	21960	7478	3729		0,88	173	28935	14618	7299
	0,90	151	22155	8303	4142		0,90	172	33120	16779	8381
	0,92	145	25485	9477	4730		0,92	171	35010	19271	9627
	0,94	145	28365	11646	5814		0,94	171	44025	25049	12516
	0,96	147	35175	15311	7647		0,96	170	53535	33237	16611
	0,98	142	41805	21140	10562		0,98	169	65205	44130	22059
1,4	0,80	164	16125	5811	2895	3,4	0,80	185	20805	9792	4886
	0,82	163	18375	6563	3272		0,82	183	22365	10685	5331
	0,84	165	18960	7109	3545		0,84	182	24360	11940	5961
	0,86	159	20340	7883	3932		0,86	182	27510	13766	6873
	0,88	155	24885	9549	4764		0,88	181	30150	15956	7968
	0,90	155	27285	11111	5544		0,90	180	33435	18249	9116
	0,92	154	31215	13101	6542		0,92	180	39465	21687	10835
	0,94	151	35985	16130	8055		0,94	179	47640	27636	13811
	0,96	150	39330	19650	9818		0,96	179	52470	33209	16598
	0,98	147	53160	29025	14505		0,98	179	68265	47916	23952
1,8	0,80	170	16470	6588	3285	3,8	0,80	192	21015	10116	5049
	0,82	168	18930	7646	3813		0,82	191	23820	11663	5822
	0,84	168	21090	8549	4265		0,84	191	25980	12936	6458
	0,86	166	22155	9393	4686		0,86	190	27780	14322	7152
	0,88	163	24585	10895	5438		0,88	190	30045	16098	8040
	0,90	162	26685	12093	6038		0,90	190	33885	19068	9525
	0,92	161	32370	15078	7529		0,92	189	38160	21702	10842
	0,94	161	34485	17627	8804		0,94	189	49395	29139	14562
	0,96	155	41730	22658	11321		0,96	189	59220	38081	19032
	0,98	145	62790	37187	18585		0,98	189	70380	51077	25532

Grafy

Předchozí graf ilustruje závislost výsledné ceny na počáteční teplotě. Je zde patrný konstantní strmý nárůst se zvyšující se počáteční teplotou. Za zmínku také stojí lokální maximum mezi teplotními body 1,8 a 2,2.

Z předcházejícího grafu, který ukazuje vliv koeficientu ochlazování na cenu řešení, je pro změnu patrný pokles se zvyšující se hodnotou koeficientu.

Další graf ukazuje závislost iterací na koeficientu ochlazování. Čím větší je tento koeficient, tím více iterací je potřeba.

Závěr

Z vizuální reprezentace výsledků pomocí grafů plynou následující závěry:

Čím vyšší počáteční teplotu nastavíme, tím lepší výsledné ceny dosáhneme
Tento růst však očividně nemůže jít do nekonečna
Pokud volíme koeficient ochlazování větší, dosahujeme nižší ceny
Čím vyšší je koeficient ochlazování, tím větší počet iterací je potřeba k řešení

Nejoptimálnějších výsledků bylo dosaženo při následujících hodnotách parametrů:

Ochlazování: α = 0.8
Počáteční teplota: T
Práh iterace 1: p = 3.8

Příloha

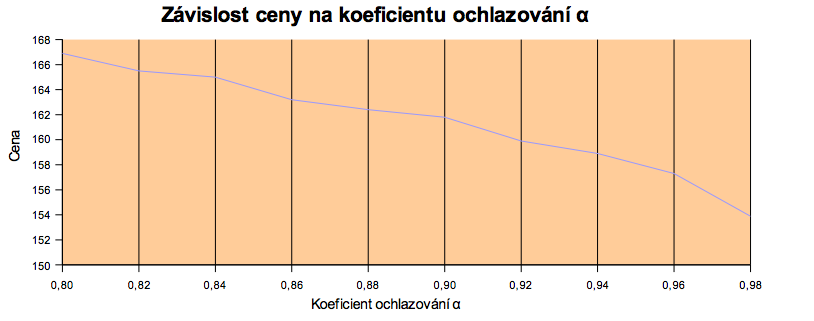
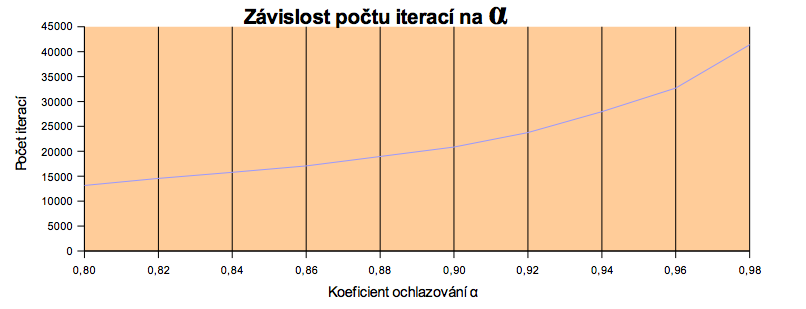
Ke stažení je k dispozici zabalená celá úloha, nebo jen zdrojový kód vytvořený v programovacím jazyku C: