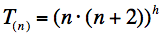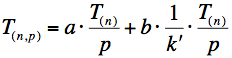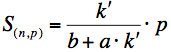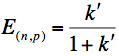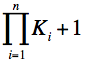Semestrální projekt PAR 2006/2007

PRV: Přelévání vody
autoři: Karel Beyr, Jan Dohnal
datum: 8. ledna 2007
5. ročník, obor výpočetní technika, K336 FEL ČVUT, Karlovo nám. 13, 121 35 Praha 2

Definice problému a popis sekvenčního řešení

Vstupní data:

n = přirozené číslo, n>=3, reprezentující počet nádob.
K[1..n] = pole prvočísel čísel z intervalu <0,1000> představující objemy (kapacity) jednotlivých nádob.
c = přirozené číslo, které je menší nebo rovno největšímu číslu z K a je různé od čísel z K

Zadáni:

Počáteční konfiguraci představuje množina n prázdných nádob s objemy K[1..n]. Dále máme neomezený zdroj vody. S libovolnou nádobou můžeme provést 2 operace

můžeme ji naplnit či doplnit libovolnou nádobu (na maximální objem).
můžeme veškerou vodu z dané nádoby vylít.

S libovolnou dvojicí nádob můžeme provést ještě třetí operaci - přelití: Při přeléváni z nádoby A do nádoby B vždy musíme buď

přelít všechnu vodu z A do B (=vyprázdnit nádobu A) nebo
dolít nádobu B na maximum (=zbytek zůstane v nádobě A)

Úkol:

Nalezněte nejkratší posloupnost operací tak, aby po jejím provedení bylo v některé nádobě c jednotek vody.

Výstup algoritmu:

Počet operací a výpis jejich posloupnosti.

Sekvenční algoritmus:

Reseni nemusi existovat (závisí na vzájemné dělitelnosti čísla c a čísel z pole K) !!! Sekvenční algoritmus je typu BB-DFS s neomezenou hloubkou prohledávání (obecně se mohou pro n>3 při prohledávání generovat cykly). Hloubku prohledávání můžeme omezit horní mezí (viz dále). Cena, kterou minimalizujeme, je počet operací. Algoritmus končí, když prohledá celý stavový prostor do hloubky dané horní mezí.

Dolní mez není za daných podmínek známa.

Horni mez na počet tahů je následující:

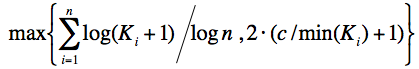
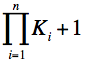
Důkaz: Hledaný výraz je hloubka n-árního stromu obsahujícího všechny prvky stavového prostoru. Velikost stavového prostoru je rovna: velikost stavoveho prostoru

Paralelní algoritmus:

Paralelní algoritmus je typu PBB-DFS-V.

Popis sekvenčního algoritmu:

Po přečtení zadání a nastavení počátečních hodnot všech kýblů na 0 a uložení těchto hodnot na zásobník probíhá vlastní výpočet: V každé iteraci se provede:

1)přečtení stavu ze zásobníku

2)kontrola, zda tento stav není konečný (dosažený objem kapaliny) - pokud ano, uložíme cestu k tomuto stavu (je nyní v pomocném zásobníku) do zásobníku kde máme uloženo nejlepší řešení. Poté aktualizujeme horní mez. Poté pokračujeme další iterací.

3)kontrola, zda tento stav není v hloubce větší než horní mez - pokud ano, stav zahodíme a startujeme další iteraci od začátku

4)následně se provedou operace pro každý kýbl: Vylití, dolítí na plno a všechna možná přelití do ostatních kýblů. (odtud n*(n+1)). Po každé iteraci se kontroluje, zda došlo ke změně stavu. Pokud ano, každý stav se uloží na zásobník.

Popis paralelního algoritmu:

Paralelní algoritmus je založen na sekvenčním s přidáním přeposílání zpráv. Nejprve procesor 0 provede 2 (obecně N) iterace na zásobníku. Potom tento zásobník pomocí ADZ rozdělí a rozešle ostatním procesorům.

Pokaždé když nějaký proces najde nejlepší řešení, rozešle zprávu všem ostatním procesům ve které jim sdělí novou nejlepší horní mez.

Když procesu dojde práce, použije algoritmus AHD pro získání práce. Dárcovský proces opět použije ADZ pro rozdělení svého zásobníku

Pro ukončení práce je použit modifikovaný Dijkstrův peškový ADUV.

Pro malé množství a velikost bylo zvoleno posílání bokujících zpráv.

Analýza složitosti paralelního řešení

Složitost sekvenčního řešení je v nejhorším případě rovna
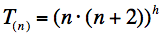
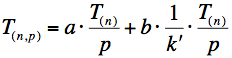
kde h je hloubka prohledávání řešení (viz. zadání) a n je počet nádob. Pro paralelní řešení můžeme stanovit složitost takto Složitost paralelního řešení
kde p je počet procesorů, druhý člen součtu představuje neustálé dotazování na zprávy, konstanty a a b vyjadřují náročnost daného sčítance (samotného výpočtu či dotazování na zprávy) a konstanta k' vyjadřuje jak často (po kolika krocích) dochází k dotazům na zprávy. Úpravami dostáváme paralelní zrychlení
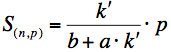
Pokud budeme považovat náročnost výpočetního kroku a dotazování na zprávy rovnou 1 (a=b=1), pak můžeme určit také efektivnost a to takto
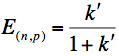
Pro velká k' (málo časté dotazy na zprávy) se bude efektivnost blížit 1 (algoritmus bude cenově optimální).

Naměřené výsledky a vyhodnocení

Zadání	sekvenční	ethernet - počet procesorů				mirinet - počet procesorů
Zadání	sekvenční	2	4	8	12	2	4	8	12
1.	126,558391	53,746896	41,595037	22,505979	21,435444	43,541153	31,456757	11,656392	10,435533
2.	298,843691	125,345586	95,455067	46,988375	7,247032	107,863556	73,953452	27,948345	3,540291
3.	578,645666	244,686605	168,645921	85,435913	88,435301	213,349482	139,503291	59,529146	65,459214

Údaj v sloupci zadání má tuto strukturu: počet kýblů (n) - hodnoty,.. (K_i) - cílový objem (c)

Graf zrychlení

Vyhodnocení

Jak je vidět z naměřených hodnot, zvyšování počtu procesorů nemusí vždy zrychlovat dobu výpočtu. Důvod je prostý - nutná obsluha při komunikaci.

V nečekaně hodně případech se nám ale podařilo docílit superlineárního zrychlení, a to především díky tomu že si procesory v průběhu práce přeposílají své výsledky a dle toho upravují horní mez.

Kdy se vyplatí použít paralelní řešení a kdy ne? V našm případě se projevila vysoká škálovatelnost problému, takže prakticky při přidání dalších procesorů došlo ke zrychlení (hranice nastává mezi 8 a 12 procesory)

Implementacni nedostatky se tykaji zejmena efektivity sekvencniho reseni: Kontrola zacykleni, lepsi heuristika a podobne by mohly vest ke zlepseni casove slozitosti, toto ale nebylo cilem projektu.

Rozdíl mezi MyriNetem a Ethernetem byl patrný u víceprocesorových aplikací. Tam dosahoval rozdílu až desítek procent.